在一棵二叉树上第5层的结点数最多是多少
请选择正确的答案。
(a)8
(b)16
(c)32
(d)15
考点:考察求职者对二叉树的掌握。
出现频率:★★★★
【面试题解析】
对于二叉树,应该掌握如下相关的知识点。
· 二叉树第i层上的结点数目最多为2i-1(i≥1)。
· 深度为k的二叉树至多有2k-1个结点(k≥1)。
· 在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则no=n2+1。
· 具有n个结点的完全二叉树的深度为log 2n+1。
满二叉树和完全二叉树是二叉树的两种特殊情形,如下所述。
1.满二叉树(FullBinaryTree)
一棵深度为k且有2k-1个结点的二叉树称为满二叉树。
满二叉树的特点如下。
· 每一层上的结点数都达到最大值。即对给定的高度,它是具有最多结点数的二叉树。
· 满二叉树中不存在度数为1 的结点,每个分支结点均有两棵高度相同的子树,且树叶都在最下一层。
图1所示是1个深度为4的特殊形态的二叉树示意图。
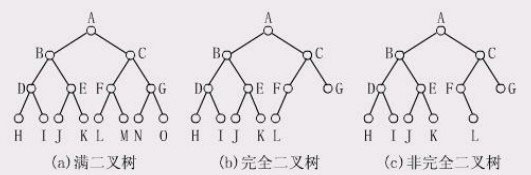
图1特殊形态的二叉树
2.完全二叉树(Complete BinaryTree)
集中在该层最左边的若干位置上,则此二叉树称为完全二叉树。完全二叉树特点如下。
· 满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
· 在满二叉树的最下一层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
· 在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。在图1(c)中,结点F没有左孩子而有右孩子L,故它不是一棵完全二叉树。图1(b)是一棵完全二叉树。根据前面对二叉树的讲解,面试题7中的个数应该是24=16。
参考答案:(b)。